In-place Circshift
Last week I was attempting to implement an in-place fftshift function in c++. I hoped this function could perform shifting along any given dimension of N-dimensional data. similar to those found in Matlab and Numpy. Interestingly, both Matlab and Numpy call another function within it, known as the circshift function in Matlab and the roll function in Numpy. These functions circularly shift the elements in an array by K positions. Below are some illustrations about what circshift does.
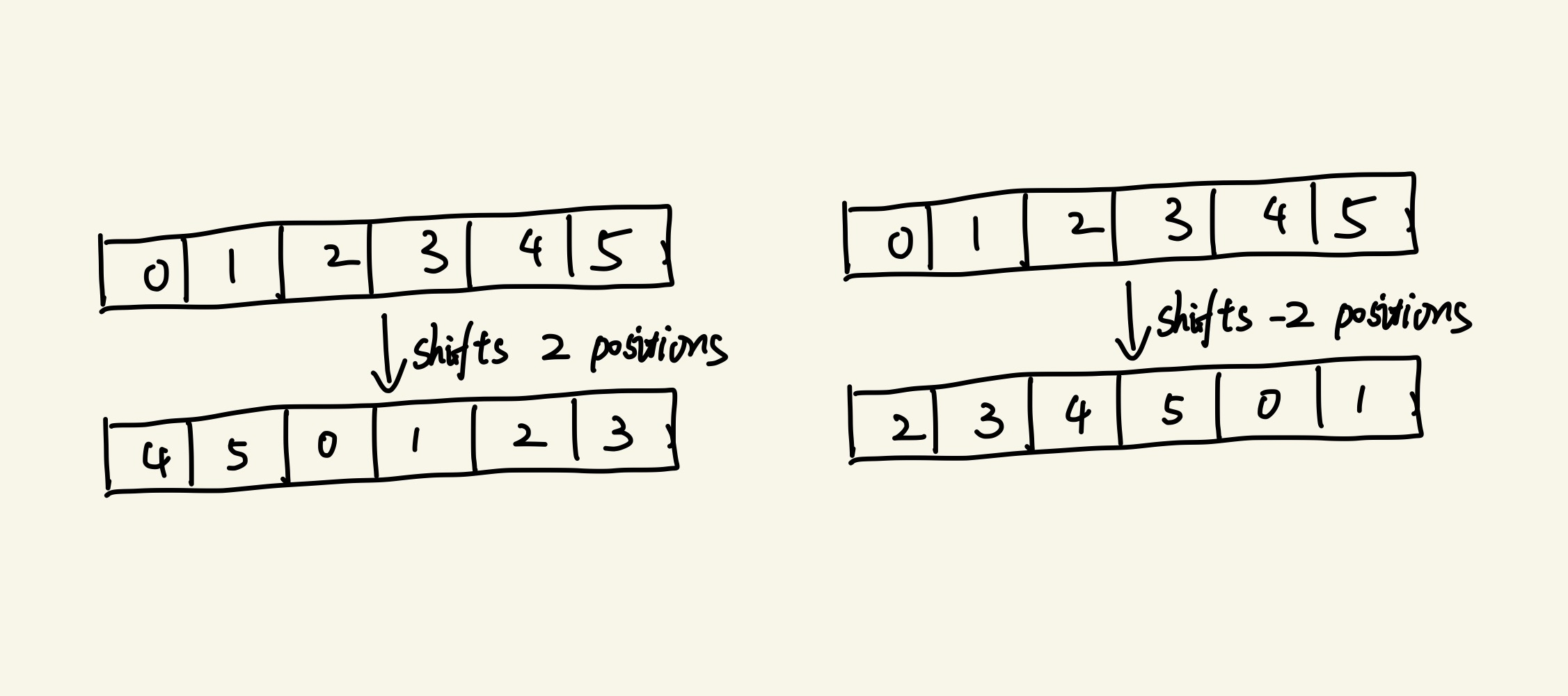
In fact, circshift is an array rotation problem that has been well-studied a few decades ago. Many problems in computer science eventually boil down to array rotation problem (That’s a rotate!). The array rotation problem is that, given an array with two parts [a, b], how to swap them to get [b, a].
Allocate and Copy
As you already know, the optimal time complexity for rotating an array is O(n), where n represents the number of elements in the array. Implementing an array rotation algorithm with a buffer is intuitive:
// left: the size of left part
// right: the size of right part
void rotate_with_buffer(int *pSrcDst, size_t left, size_t right)
{
int* pBuffer = new int[left + right];
// copy left-side elements to buffer
memcpy(pBuffer, pSrcDst, left * sizeof(int));
// copy right-side elements to the beginning
memmove(pSrcDst, pSrcDst+left, right * sizeof(int));
// copy buffer to the rest positions
memcpy(pSrcDst+right, pBuffer, left * sizeof(int));
delete[] pBuffer;
}
Bridge Rotation
rotation_with_buffer is quite simple, provided that you can pay for the cost of memory allocation. In fact, for small arrays, it may outperform other algorithms. Memory requirements can be further reduced by considering the overlap of two parts:
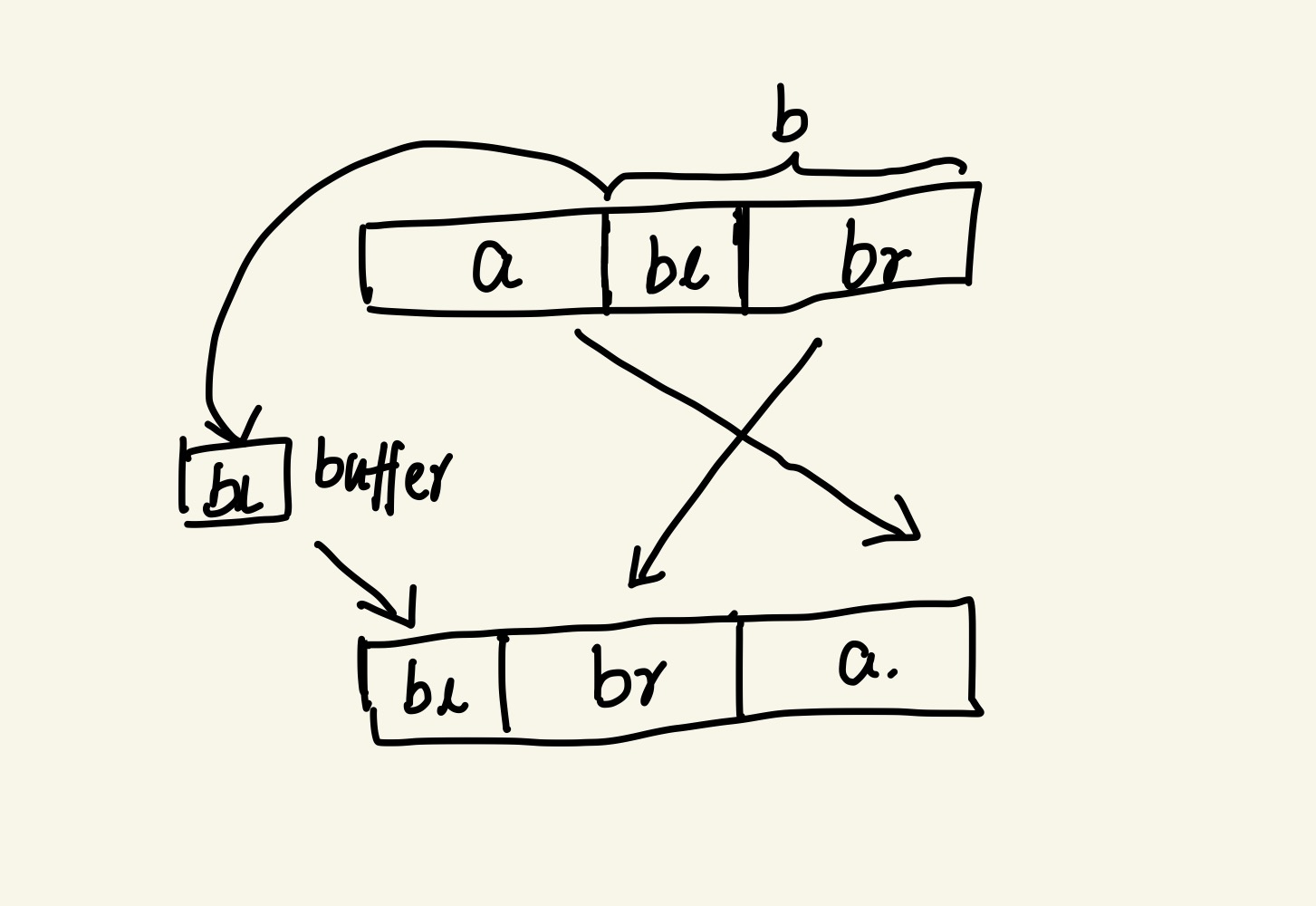
Here we divide the array into three parts (assuming a is smaller than b): bl, which represents the overlap of a and b ,and the size of a equals to the size of br. If bl is smaller than a, then we move bl to the buffer and sequentially shift br and a to their correct positions. Finally, we move bl back to the beginning of array. If bl is bigger than a, then we revert to the previous algorithm, buffering a instead. The basic idea is that we always move the smallest part to the buffer. Hoven called it a bridge rotation algorithm.
Triple Reversal Rotation
Obviously, the above two are not turly in-place rotation. Triple reversal algorithm, as found in Programming Pearls, 2nd Edition, is a prime example of an in-place algorithm. It’s remarkably elegant and easy to understand. Let me explain this algorithm with some notations: $ab$ denotes the array to be rotated, $ba$ is the result of rotation, $a^r$ is the reversal of $a$, $b^r$ is the reversal of $b$. It’s straightforward to infer two theorems: $(a^r)^r = a$, and $(ab)^r = b^ra^r$ (it looks like the tranpose in matrix multiply!).
To get $ba$ with reverse operations, we have the following chains:
- $ab \rightarrow a^rb \rightarrow a^rb^r \rightarrow (a^rb^r)^r = ba$
- $ab \rightarrow ab^r \rightarrow a^rb^r \rightarrow (a^rb^r)^r = ba$
- $ab \rightarrow (ab)^r=b^ra^r \rightarrow ba^r \rightarrow ba$
- $ab \rightarrow (ab)^r=b^ra^r \rightarrow b^ra \rightarrow ba$
We can rotate the array with only three reverse operations in many ways. Here is one of implementations:
// reverse array pSrcDst with N elements
void reverse(int* pSrcDst, size_t N)
{
int *pa, *pb;
pa = pSrcDst;
pb = pSrcDst + N;
N /= 2;
for (size_t i = 0; i < N; ++i)
{
int buffer = *(pa + i);
*(pa + i) = *(pb - i - 1);
*(pb - i - 1) = buffer;
}
}
// left: the size of left part
// right: the size of right part
void reversal_rotate(int *pSrcDst, size_t left, size_t right)
{
reverse(pSrcDst, left);
reverse(pSrcDst + left, right);
reverse(pSrcDst, left + right);
}
Triple reversal rotation involves precisely 2N memory operations. Hoven proposed an enhanced version, named trinity rotation, which improves locality and reduces the number of moves. Honestly, I don’t really grasp the idea behind this algorithm and it seems quite complicated. If you are curious, please explore Hoven’s page. Additionally, the performance of triple reversal also depends on how to implement a reverse function efficiently. This blog provides a detailed explanation on how to implement it, utilizing modern computer characteristics, resulting in up to x22 speedups compared to std::reverse in the standard C++ library!
Performance Test
I compared the perfomance of bridge rotation, triple reversal rotation, and conjoint reversal rotation (aka trinity rotation) on my PC. It’s not a rigorous test. The array size is 1000000, and I chose the left to be 333334. I ran each rotation algorithm 100 times to compute the average running time. I was expecting bridge rotation to be the worst since it had to allocate memory for one third of the array size. Surprisingly, they got nearly the same performance (bridge rotation: 253.5us, triple reversal rotation: 255.6us, conjoint reversal rotation: 252.6us).
How operation system optimizs memory management may contribute to this phenomenon. If I just freed allocated memory at the end of each loop and then executed the next loop immediately, I found that the first iteration cost much longer time (1000us) and the subsequent iterations cost shorter time (200-300us). If I deliberately didn’t free the buffer in each rotation, as recommended in this blog, bridge rotation was worse than the others. I can imagine that the system reuses the same memory block in each iteration, thereby making the time for memory allocation within subsequent iterations negligible. The blog I mentioned before also compared a juggling rotation with triple reversal rotation, and it found that most rotation algorithms are almost at the same level. The best way to optimize such an algorithm is to make it as predictable as possible for modern computers so that they can utilize their hardware-level advantages to accelerate the program. It does make sense.
Circshift
Here I use triple reversal rotation to implement an in-place circshift function capable of shifting along any given dimension of N-dimensional data. The code is here and the interface looks like this:
void circshift(const std::vector<int> &vDims, int iAxis, int shift, T *pSrcDst);
It’s not a fully optimized algorithm since I use two loops to handle data before and after the target axis seperately. I compared its performance with Matlab’s built-in circshift function, and Matlab is still faster in small and medium array sizes. However, as the size grows larger, it takes much longer for Matlab to allocate a buffer for shifted elements. In such cases, this naive in-place circshift can outperform it.
Fftshift
Once you get circshift, fftshift and ifftshift are quite easy to implement:
template <typename T>
void fftshift(const std::vector<int>& vDims, int iAxis, T* pSrcDst)
{
int K = vDims[iAxis] / 2;
circshift(vDims, iAxis, K, pSrcDst);
}
template <typename T>
void ifftshift(const std::vector<int>& vDims, int iAxis, T* pSrcDst)
{
int K = (vDims[iAxis] - 1) / 2 + 1;
circshift(vDims, iAxis, K, pSrcDst);
}