主成分分析PCA
主成分分析(Principle Component Analysis,PCA)是常用的一种矩阵分解算法,PCA通过旋转原始空间来使得数据在各个正交轴上的投影最大,通过选择前几个正交轴可以实现数据降维的目的。
PCA数学原理
优化问题
PCA的优化问题如下:
\[\DeclareMathOperator*{\argmax}{arg\,max} \begin{equation} \begin{split} \argmax_{\mathbf{W}}\quad &\mathrm{trace}\left(\mathbf{W}^T\mathbf{X}\mathbf{X}^T\mathbf{W}\right)\\ \textrm{s.t.}\quad &\mathbf{W}^T\mathbf{W} = \mathbf{I} \end{split} \end{equation}\]其中$\mathbf{X} \in \mathbb{R}^{M \times N}$是数据,$\mathbf{W} \in \mathbb{R}^{M \times M}$是投影矩阵,$N$是样本点个数,$M$是特征个数。PCA要求数据$\mathbf{X}$做零均值处理,优化问题的解可以转化为如下特征值分解问题的解:
\[\begin{equation} \left(\mathbf{X}\mathbf{X}^T\right)\mathbf{W} = \mathbf{W}\mathbf{\Lambda} \end{equation}\]这里假设$\mathbf{W}$的列向量按相应特征值的大小从大到小排列,保留$\mathbf{W}$前K列即前K个成分的列向量$\hat{\mathbf{W}}$,降维后的数据特征为:
\[\begin{equation} \hat{\mathbf{X}} = \hat{\mathbf{W}}^T\mathbf{X} \end{equation}\]其中$\hat{\mathbf{X}} \in \mathbb{R}^{K \times N}$。
实现分析
svd替代eig
sklearn中的PCA实现并未使用eig而是使用svd,主要原因是svd比eig具有更好的数值稳定性(当然代价是其计算时间要比eig更长)。使用svd代替eig也是很多学者如Andrew Ng建议的策略,在StackExchange上也有关于svd和eig的相关讨论讨论1、讨论2。sklearn中直接对数据矩阵$\mathbf{X}$而不是协方差矩阵$\mathbf{X}\mathbf{X}^T$做svd,其等价关系如下:
\[\begin{equation} \begin{split} \mathbf{X} &= \mathbf{U} \mathbf{\Sigma} \mathbf{V}^T\\ \mathbf{X}\mathbf{X}^T &= \mathbf{U} \mathbf{\Sigma}^2 \mathbf{U}^T\\ \mathbf{W} &= \mathbf{U}\\ \mathbf{\Lambda} &= \mathbf{\Sigma}^2 \end{split} \end{equation}\]sign ambiguity问题
sklearn的PCA代码中还考虑了svd的sign ambiguity问题,即每个奇异向量的符号在求解过程中是不确定的(例如,将$\mathbf{u}_k$和$\mathbf{v}_k$同时乘以-1也满足求解条件)。svd算法(包括eig)中的奇异向量符号只是确保数值稳定性的副产品,类似随机分配符号,并无实际意义。
sklearn使用svd_flip(u, v, u_based_descision=True)函数来确保输出确定性的奇异向量符号,例如,如果u_based_decision=True,则要求$\mathbf{U}$的每一列奇异向量中绝对值最大的元素的符号始终为正,$\mathbf{V}$也要相对的做出调整。
鉴于MATLAB是算法开发的标准之一,我很好奇MATLAB是如何处理SVD的sign ambiguity问题的。MATLAB的svd函数的官方文档中有这样一句话:
Different machines and releases of MATLAB® can produce different singular vectors that are still numerically accurate. Corresponding columns in U and V can flip their signs, since this does not affect the value of the expression A = USV’.
MATLAB的eig函数的官方文档中亦提到:
For real eigenvectors, the sign of the eigenvectors can change.
可以看出MATLAB也未保证符号的确定性。同样在MATALB的社区里也有人问了这个问题,并引导我看了这篇Resolving the Sign Ambiguity in the Singular Value Decompostion的文献。
文献中指出,sklearn的svd_flip方法是一种临时方案(ad hoc),并未从数据分析或者解释的角度来解决sign ambiguity问题。解决sign ambiguity的核心是如何为奇异向量选择一个“有意义”的符号。什么叫“有意义”?比方说我们要研究4种品牌汽车的每公里耗油量,做了4次抽样,构成数据矩阵:
其中每一列是一种品牌汽车的耗油量,每一行为抽样情况,svd分解有$\mathbf{X}=\mathbf{U} \mathbf{\Sigma} \mathbf{V}^T$。我们来看一下numpy.linalg.svd计算得到的$\mathbf{V}$的第一个奇异向量:
$\mathbf{v}_0$实际指明了耗油量空间的一个向量,然而我们知道耗油量没有负值(如果有的话人类就拥有无限能源了),一个完全指向负的方向意义不大,如果改变$\mathbf{v}_0$的符号,变为:
\[\begin{equation} \begin{split} \mathbf{v}_0 = \begin{bmatrix} 0.15 \\ 0.96 \\ 0.14 \\ 0.20 \\ \end{bmatrix} \end{split} \end{equation}\]结果就合理多了。
文献中指出,奇异向量的符号应当与大多数数据样本向量的符号相同,从几何上来看,奇异向量应当指向大多数向量指向的方向。下图是我从文献中截取的,深色蓝线是正确的奇异向量方向,浅色蓝线是数据向量。
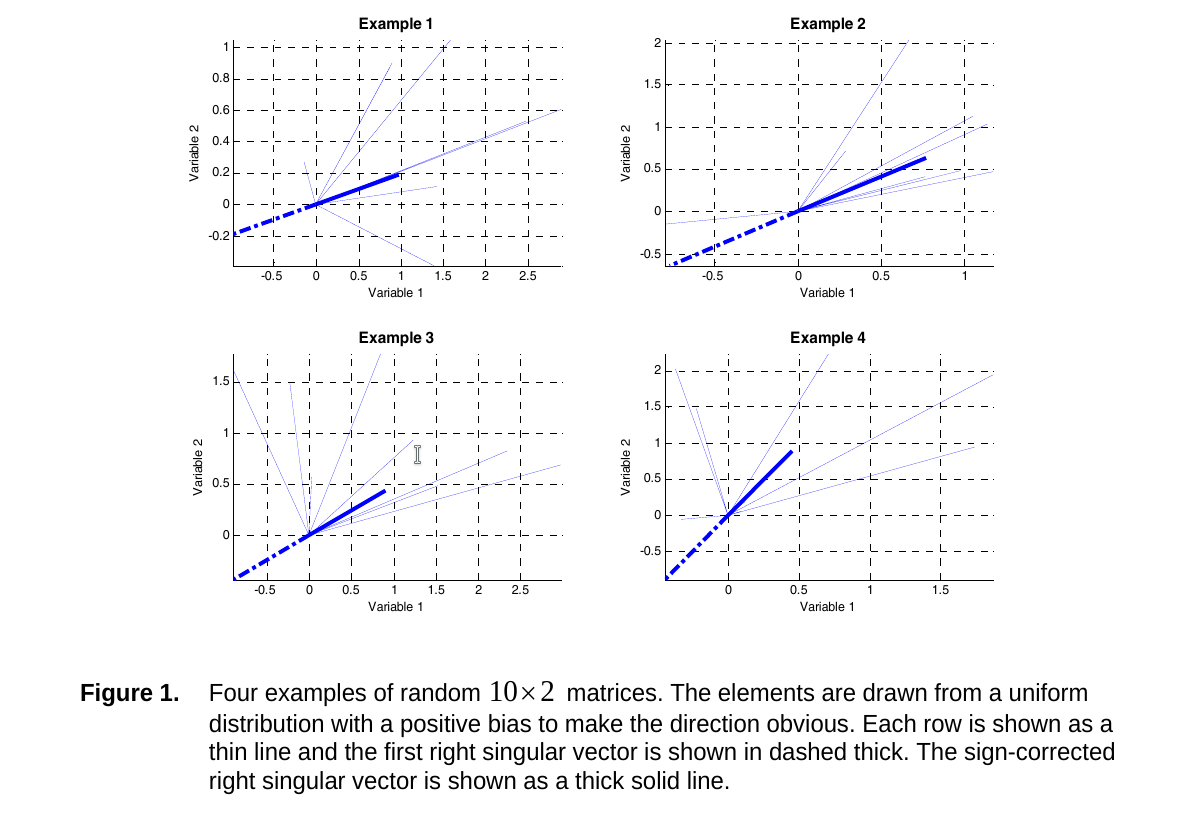
翻译成数学语言(我按照自己的理解和习惯转化成优化问题,与文献的原始表述并不一致,不一定对,有兴趣的读者可以看原始文献),纠正符号算法的核心是对于每一对奇异向量$\mathbf{u}_k$和$\mathbf{v}_k$,寻找符号$s_k$优化以下目标函数
\[\begin{equation} \argmax_{s_k \in \{1,-1\}}\quad s_k \left(\sum_{j=1}^N \mathbf{u}_k^T\mathbf{X}_{\cdot,j} + \sum_{i=1}^M\mathbf{X}_{i,\cdot}\mathbf{v}_k\right) \end{equation}\]根据两项求和项的符号即可决定$s_k$的符号。对于可能存在的左右奇异向量符号冲突的情况(例如单独看左奇异向量有意义的符号是-1,单独看右奇异向量有意义的符号为1),该算法选择以求和绝对值最大的一项的符号为主(反应在上式就是两项求和)。文献中指出,该算法仅在上述求和项不为0的情况下有效(即在0附近奇异向量的符号可以为任意情况)。
Python版具体算法实现如下,Matlab可以使用这个版本:
import warnings
import numpy as np
def sign_flip(u, s, vh=None):
"""Flip signs of SVD or EIG.
"""
left_proj = 0
if vh is not None:
left_proj = np.sum(s[:, np.newaxis]*vh, axis=-1)
right_proj = np.sum(u*s, axis=0)
total_proj = left_proj + right_proj
signs = np.sign(total_proj)
random_idx = (signs==0)
if np.any(random_idx):
signs[random_idx] = 1
warnings.warn("The magnitude is close to zero, the sign will become arbitrary.")
u = u*signs
if vh is not None:
vh = signs[:, np.newaxis]*vh
return u, s, vh