This post summarizes the ESPIRiT algorithm for estimating coil sensitivies in MRI. It took me months to grasp the theory behind it.

A short introduction

MRI is a common imaging technique for medical diagnosis nowadays. It’s nearly harmless for humans in contrast to other radioactive imaging techniques. In MRI, when a patient is exposed to a magnetic field, hydrogen atoms align with the field. This alignment could be disrupt by a radiofrequency pulse. As the atoms return to their original alignment, they emit signals captured by sensors and used to create medical images.

The signals captured by a sensor cc (or coil cc) can be approximately formulated as:

yc(k⃗(t))=∫x(r⃗)Bc(r⃗)e−i2πk⃗(t)⋅r⃗dr⃗\begin{equation} \begin{split} y_c(\vec{k}(t)) = \int x(\vec{r}) B_{c}(\vec{r}) e^{-i 2 \pi \vec{k}(t)\cdot\vec{r}}d\vec{r} \end{split} \end{equation}

where x(r⃗)x(\vec{r}) is an unkown tissue value at location r⃗\vec{r}, Bc(r⃗)B_{c}(\vec{r}) is some value related to the receiver coil cc, often named as coil sensitivities, k⃗(t)\vec{k}(t) is k-space coordinates along with the time tt. It’s common to have dozens of coils in clinical settings.

This formula indicates that the signals captured by the coil cc are fourier transform of interested tissue values which are multipled by the sensitivity map of the coil cc. A concise way of the above formula is to represent it with operators:

yc=FScx\begin{equation} \begin{split} y_c = \mathcal{F}\mathcal{S}_cx \end{split} \end{equation}

where F\mathcal{F} denotes fourier transform, Sc\mathcal{S}_c denotes the sensitivity map of the coil cc, ycy_c and xx are both vectorized.

Most of the time, coil sensitivities are not available beforehand. We have to estimate them from acquired signals. ESPIRiT is such a method for estimating coil sensitivities , supported by soild theoretical analysis.

About GRAPPA

Before diving into ESPIRiT, it’s important to first understand GRAPPA, a well-established parallel imaging method used in MRI. The core of GRAPPA is to interpolate missing k-space points by linearly weighting neighboring acquired points, with the weighting coefficients determined from the calibration region.

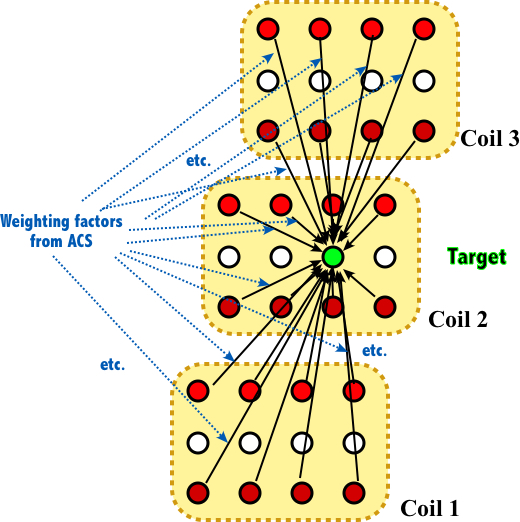
Again, a concise way to describe GRAPPA is using operators:

xc(r)=(PkRry)Tgc\begin{equation} \begin{split} x_c(r) = (\mathcal{P}_{k}\mathcal{R}_ry)^T \mathbf{g}_{c} \end{split} \end{equation}

where yy represents the vectorized multicoil k-space data with unacquired data set to zero, xc(r)x_c(r) is the estimated value for coil cc at location rr (for simplicity, the vector notation is omitted, but keep in mind that rr is a discrete spatial vector index), gc\mathbf{g}_c denotes weighting coefficients for coil cc, Rr\mathcal{R}_r is a patch operator that selects a local block of data around location rr and Pk\mathcal{P}_k is a sampling operator that selects only the acquired points within the patch (the subscript kk implies that there may exist many sampling patterns).

We can easily construct linear equations using the data from the calibration region, with the same undersamping pattern Pk\mathcal{P}_k:

ycAC=APkTgc\begin{equation} \begin{split} \mathbf{y}_c^{AC} = \mathbf{A}\mathcal{P}_k^T\mathbf{g}_c \end{split} \end{equation}

where ycAC\mathbf{y}_c^{AC} denotes the vectorized data in the calibration region, A\mathbf{A} is a so-called calibration matrix, that each row is a local patch around the current acquired point. In this case, gc\mathbf{g}_c can be efficiently solved by many numerical methods.

By construction , one of the columns of A\mathbf{A} is actually ycAC\mathbf{y}_c^{AC} itself. Write this as Aec=ycAC\mathbf{A}\mathbf{e}_c = \mathbf{y}_c^{AC}, where ec\mathbf{e}_c is a vector with 1 in the appropriate location to select the corresponding column of A\mathbf{A}. We note that:

APkTgc−ycAC=0APkTgc−Aec=0A(PkTgc−ec)=0\begin{equation} \begin{split} \mathbf{A}\mathcal{P}_k^T\mathbf{g}_c - \mathbf{y}_c^{AC} &= 0\\ \mathbf{A}\mathcal{P}_k^T\mathbf{g}_c - \mathbf{A}\mathbf{e}_c &= 0\\ \mathbf{A}(\mathcal{P}_k^T\mathbf{g}_c - \mathbf{e}_c) &= 0 \end{split} \end{equation}

The existence of null-space implies redundancy in row-space of A\mathbf{A}. gc\mathbf{g}_c in GRAPPA are very specific null-space vectors. Instead of using this specific form, ESPIRiT analyzes the calibration matrix A\mathbf{A} directly.

Key assumptions in ESPIRiT

Since the matrix A\mathbf{A} is constructed using local patches in the calibration region, ESPIRiT assumes that all patches, whether in the calibration region or not, lie in the row-space of A\mathbf{A}:

V⊥TRrx=0,∀r\begin{equation} \begin{split} \mathbf{V}_{\perp}^T\mathcal{R}_r \mathbf{x} &= \mathbf{0}, \quad \forall r \end{split} \end{equation}

where V⊥\mathbf{V}_{\perp} is the basis that spans the null-space and x\mathbf{x} is the vectorized multicoil k-space data. Note that “lying in the row-space” is equivalent to being orthogonal to the null-space.

I wrote the formula as V⊥HRrx\mathbf{V}_{\perp}^H\mathcal{R}_r \mathbf{x}, following the same notation used in the paper. However, this ultimatley leads to an algorithm that conflicts with most correct implementations, which require flipping the kernels before applying the Fourier transform. Neither the paper nor subsequent research discussed this operation in detail. This confused me for months and it was truly frustrating.

I think the mismatch arises from how we handle the inner product of complex vectors. The rows of the matrix A are flattened row vectors extracted from local patches, while Rrx\mathcal{R}_r \mathbf{x} is a flattened column vector.

Since the standard Hermitian inner product is defined for column vectors, when we want to compute the inner product of two row vectors a,b∈C1×N\mathbf{a}, \mathbf{b} \in \mathbb{C}^{1 \times N}, we firstly convert them into column vectors:

⟨a,b⟩=⟨aT,bT⟩=(aT)HbT=a∗bT\begin{equation} \begin{split} \langle \mathbf{a}, \mathbf{b} \rangle = \langle \mathbf{a}^T, \mathbf{b}^T \rangle = (\mathbf{a}^T)^H\mathbf{b}^T = \mathbf{a}^*\mathbf{b}^T \end{split} \end{equation}

Thus the inner product of V⊥H\mathbf{V}_{\perp}^H and Rrx\mathcal{R}_r \mathbf{x} is V⊥TRrx\mathbf{V}_{\perp}^T\mathcal{R}_r \mathbf{x} instead of V⊥HRrx\mathbf{V}_{\perp}^H\mathcal{R}_r \mathbf{x} from the original paper.

V⊥\mathbf{V}_{\perp} is computed by singular value decomposition of A\mathbf{A}:

A=UΣVH=UΣ[V∥V⊥]H\begin{equation} \begin{split} \mathbf{A} &= \mathbf{U} \mathbf{\Sigma} \mathbf{V}^H\\ &= \mathbf{U} \mathbf{\Sigma} \begin{bmatrix} \mathbf{V}_{\parallel} & \mathbf{V}_{\perp} \end{bmatrix}^H \end{split} \end{equation}

where V∥\mathbf{V}_{\parallel} corresponds to non-zero singular values and V⊥\mathbf{V}_{\perp} corresponds to zero singular values.

Solving the nullspace constraint in the least-square framework

arg min⁡x∑r12∥V⊥TRrx∥F2% \DeclareMathOperator*{\argmin}{arg\,min} \begin{equation} \begin{split} \argmin_{\mathbf{x}} \quad \sum_{r} \frac{1}{2} \|\mathbf{V}_{\perp }^T \mathcal{R}_r \mathbf{x}\|_F^2 \end{split} \end{equation}

which leads to the following equations by zeroing out the gradient:

∑rRrH(V⊥V⊥H)∗Rrx=0\begin{equation} \begin{split} \sum_r \mathcal{R}_r^H\left(\mathbf{V}_{\perp}\mathbf{V}_{\perp}^H\right)^*\mathcal{R}_r\mathbf{x} = \mathbf{0} \end{split} \end{equation}

Since V\mathbf{V} is unitary, we have I=V⊥V⊥H+V∥V∥H\mathbf{I} = \mathbf{V}_{\perp}\mathbf{V}_{\perp}^H + \mathbf{V}_{\parallel}\mathbf{V}_{\parallel}^H. By substituting into the above equations, we get:

∑rRrH(V∥V∥H)∗Rrx=∑rRrHRrx\begin{equation} \begin{split} \sum_r \mathcal{R}_r^H\left(\mathbf{V}_{\parallel}\mathbf{V}_{\parallel}^H\right)^*\mathcal{R}_r\mathbf{x} = \sum_r \mathcal{R}_r^H\mathcal{R}_r \mathbf{x} \end{split} \end{equation}

The effect of RrHRr\mathcal{R}_r^H\mathcal{R}_r is to restore the patch to its original location while zeroing out others elements. The overall effect of ∑rRrHRr\sum_r \mathcal{R}_r^H\mathcal{R}_r is a diagonal matrix, where each diagonal element equals to MM, indicating the number of times it appears in the neighboring patches. With MM, the equation can be transformed to:

M−1∑rRrH(V∥V∥H)∗Rrx=x\begin{equation} \begin{split} M^{-1}\sum_r \mathcal{R}_r^H\left(\mathbf{V}_{\parallel}\mathbf{V}_{\parallel}^H\right)^*\mathcal{R}_r\mathbf{x} = \mathbf{x} \end{split} \end{equation}

which is equation (9) in the paper except for the conjugation.

“Obvious” convolution

The most challenging part for me is to derive equation (16) Gqs⃗q=s⃗q\mathcal{G}_q \vec{s}_q = \vec{s}_q from the paper. The authors mentioned that the operator W=M−1∑rRrHV∥V∥HRr\mathcal{W} = M^{-1}\sum_r \mathcal{R}_r^H\mathbf{V}_{\parallel}\mathbf{V}_{\parallel}^H\mathcal{R}_r (in our case, W=M−1∑rRrH(V∥V∥H)∗Rr\mathcal{W} = M^{-1}\sum_r \mathcal{R}_r^H\left(\mathbf{V}_{\parallel}\mathbf{V}_{\parallel}^H\right)^*\mathcal{R}_r) is a matrix-valued convolution, which can be decoupled into point-wise matrix operations in the image domain. The sensitivity maps are obtained by the eigenvalue decomposition of all Gq\mathcal{G}_q’s choosing only the eigenvectors corresponding to eigenvalue “=1”.

The intutive is that we could use the Fourier Convolution Theorem to get what we want, which is more straightforward in scalar cases. However, since W\mathcal{W} is a high-dimensional operator (k-space locations and channels), applying the theorem directly is not straightforward. A better approach would be to transform W\mathcal{W} into a form that resembles something familiar in 1D.

To simplify the derivation, we first introduce some notations:

  • P=(V∥V∥H)∗\mathbf{P} =\left(\mathbf{V}_{\parallel}\mathbf{V}_{\parallel}^H\right)^*: P\mathbf{P} operates on patches
  • P(c,α),(d,β)\mathbf{P}_{(c,\alpha), (d, \beta)}: a scalar value, where (c,α)(c,\alpha) represents the c-th channel and location α\alpha in the output (row index), and (d,β)(d, \beta) represents the dd-th channel and location β\beta in the input (column index)
  • xc(r)\mathbf{x}_c(r): a scalar value, where cc represents the cc-th channel and rr reprsents location rr in the k-space
  • (Rrx)(d,β)(\mathcal{R}_r\mathbf{x})_{(d, \beta)}: a scalar value, the dd-th coil value at location β\beta in the patch centered at location rr
  • (PRrx)(c,α)(\mathbf{P}\mathcal{R}_r\mathbf{x})_{(c,\alpha)}: a scalar value, the cc-th coil value at location α\alpha of the output
  • (RrHPRrx)c(m)(\mathcal{R}_r^H\mathbf{P}\mathcal{R}_r\mathbf{x})_c(m): a scalar value, the cc-th coil value at location mm in the k-space

As we have discussed above, Rr\mathcal{R}_r extracts a patch centered at location rr:

(Rrx)(d,β)=xd(r+β)\begin{equation} \begin{split} (\mathcal{R}_r\mathbf{x})_{(d,\beta)}=\mathbf{x}_d(r+\beta) \end{split} \end{equation}

where β\beta represents the relative shift with respect to the central location rr.

The effect of P\mathbf{P} is to perform a weighted summation across the channels and locations of the input:

(PRrx)(c,α)=∑d,βP(c,α),(d,β)(Rrx)(d,β)=∑d,βP(c,α),(d,β)xd(r+β)\begin{equation} \begin{split} (\mathbf{P}\mathcal{R}_r\mathbf{x})_{(c,\alpha)} &= \sum_{d,\beta}\mathbf{P}_{(c,\alpha), (d, \beta)} (\mathcal{R}_r\mathbf{x})_{(d,\beta)}\\ &= \sum_{d,\beta}\mathbf{P}_{(c,\alpha), (d, \beta)}\mathbf{x}_d(r+\beta) \end{split} \end{equation}

The effect of RrH\mathcal{R}_r^H is to restore the patch to its original location while zeroing out others elements:

(RrHPRrx)c(m)=∑αδ(m,r+α)(PRrx)(c,α)\begin{equation} \begin{split} (\mathcal{R}_r^H\mathbf{P}\mathcal{R}_r\mathbf{x})_c(m) &= \sum_{\alpha} \delta(m, r+\alpha)(\mathbf{P}\mathcal{R}_r\mathbf{x})_{(c,\alpha)} \end{split} \end{equation}

where δ(⋅,⋅)\delta(\cdot, \cdot) is the Kronecker delta function, which plays an important role in eliminating the inner α\alpha.

With these notations, we have:

(Wx)c(m)=M−1∑r(RrHPRrx)c(m)=M−1∑r∑αδ(m,r+α)(PRrx)(c,α)=M−1∑r∑αδ(m,r+α)∑d,βP(c,α),(d,β)xd(r+β)=M−1∑α,d,β∑rδ(m,r+α)P(c,α),(d,β)xd(r+β)\begin{equation} \begin{split} (\mathcal{W}\mathbf{x})_c(m) &= M^{-1}\sum_r (\mathcal{R}_r^H\mathbf{P}\mathcal{R}_r\mathbf{x})_c(m)\\ &= M^{-1}\sum_r\sum_{\alpha} \delta(m, r+\alpha)(\mathbf{P}\mathcal{R}_r\mathbf{x})_{(c,\alpha)}\\ &= M^{-1}\sum_r\sum_{\alpha} \delta(m, r+\alpha)\sum_{d,\beta}\mathbf{P}_{(c,\alpha), (d, \beta)}\mathbf{x}_d(r+\beta)\\ &=M^{-1}\sum_{\alpha,d,\beta}\sum_r\delta(m, r+\alpha)\mathbf{P}_{(c,\alpha), (d, \beta)}\mathbf{x}_d(r+\beta) \end{split} \end{equation}

Since δ(m,r+α)=1\delta(m,r+\alpha) = 1 if and only if m=r+αm=r+\alpha, we further have:

(Wx)c(m)=M−1∑α,d,βP(c,α),(d,β)xd(m−(α−β))\begin{equation} \begin{split} (\mathcal{W}\mathbf{x})_c(m) &= M^{-1}\sum_{\alpha,d,\beta}\mathbf{P}_{(c,\alpha), (d, \beta)}\mathbf{x}_d(m - (\alpha-\beta)) \end{split} \end{equation}

Let u=α−βu=\alpha - \beta represents the difference between the relative shifts, then:

(Wx)c(m)=M−1∑d∑u(∑α,β,α−β=uP(c,α),(d,β))xd(m−u)=M−1∑d∑uKc,d(u)xd(m−u)\begin{equation} \begin{split} (\mathcal{W}\mathbf{x})_c(m) &= M^{-1}\sum_{d} \sum_u (\sum_{\alpha,\beta,\alpha - \beta= u}\mathbf{P}_{(c,\alpha), (d, \beta)})\mathbf{x}_d(m - u)\\ &=M^{-1}\sum_{d} \sum_u \mathbf{K}_{c,d}(u)\mathbf{x}_d(m - u) \end{split} \end{equation}

where Kc,d(u)=∑α,β,α−β=uP(c,α),(d,β)\mathbf{K}_{c,d}(u) = \sum_{\alpha,\beta,\alpha - \beta= u}\mathbf{P}_{(c,\alpha), (d, \beta)}. Recall that uu is determined by the relative shifts of α\alpha and β\beta. What we are doing here is actually re-grouping the pairs (α,β)(\alpha, \beta) according to their common difference uu. We don’t need to worry about how to compute Kc,d(u)\mathbf{K}_{c,d}(u) right now; we only need to understand that it is a scalar value associated with c,dc,d and the difference uu.

Finally, we got something that looks like a convolution. ∑uKc,d(u)xd(m−u)\sum_u \mathbf{K}_{c,d}(u)\mathbf{x}_d(m - u) is a convolution of Kc,d(m)\mathbf{K}_{c,d}(m) and xd(m)\mathbf{x}_d(m). It’s worth noting that uu cannot exceed twice the size of the patch, as it represents the difference between the relative shifts. Kc,d(m)\mathbf{K}_{c,d}(m) is only meaningful in this range.

Calculate coil sensitivies

We should know that xc(m)=F[sc(n)x^(n)](m)\mathbf{x}_c(m)=\mathcal{F}[\mathbf{s}_c(n)\hat{\mathbf{x}}(n)](m), as we have discussed in the introduction. Let’s add it to the right-hand side of the equation:

(Wx)c(m)=xc(m)M−1∑dKc,d(m)∗xd(m)=xc(m)\begin{equation} \begin{split} (\mathcal{W}\mathbf{x})_c(m) &= \mathbf{x}_c(m)\\ M^{-1}\sum_{d} \mathbf{K}_{c,d}(m) \ast\mathbf{x}_d(m) &= \mathbf{x}_c(m)\\ \end{split} \end{equation}

Apply the inverse Fourier transform on both sides:

M−1∑dK^c,d(n)sd(n)x^(n)=sc(n)x^(n)\begin{equation} \begin{split} M^{-1}\sum_{d} \hat{\mathbf{K}}_{c,d}(n)\mathbf{s}_d(n)\hat{\mathbf{x}}(n) &= \mathbf{s}_c(n)\hat{\mathbf{x}}(n)\\ \end{split} \end{equation}

where x^(n)\hat{\mathbf{x}}(n) is in image-space, sd(n)\mathbf{s}_d(n) is the dd-th coil sensitivity value at the location nn. With all coils at the location nn, we have:

M−1[K^1,1(n)⋯K^1,Nc(n)⋮⋱⋮K^Nc,1(n)⋯K^Nc,Nc(n)][s1(n)⋮sNc(n)]x^(n)=[s1(n)⋮sNc(n)]x^(n)\begin{equation} \begin{split} M^{-1} \begin{bmatrix} \hat{\mathbf{K}}_{1,1}(n) & \cdots & \hat{\mathbf{K}}_{1,N_c}(n)\\ \vdots & \ddots & \vdots\\ \hat{\mathbf{K}}_{N_c,1}(n) & \cdots & \hat{\mathbf{K}}_{N_c,N_c}(n)\\ \end{bmatrix} \begin{bmatrix} \mathbf{s}_1(n)\\ \vdots\\ \mathbf{s}_{N_c}(n)\\ \end{bmatrix} \hat{\mathbf{x}}(n) &= \begin{bmatrix} \mathbf{s}_1(n)\\ \vdots\\ \mathbf{s}_{N_c}(n)\\ \end{bmatrix} \hat{\mathbf{x}}(n) \end{split} \end{equation}

where x^(n)\hat{\mathbf{x}}(n) can be eliminated if it is non-zero.

Now it’s clear that the coil sensitivities at location nn are the eigenvectors corresponding to the eigenvalues equal to 1.

The remaining question is what the inverse Fourier transform of K^c,d(n)\hat{\mathbf{K}}_{c,d}(n) is:

K^c,d(n)=1N∑mKc,d(m)ei2πnmN=1N∑m∑α,β,α−β=mP(c,α),(d,β)ei2πnmN=1N∑α,βP(c,α),(d,β)ei2πn(α−β)N\begin{equation} \begin{split} \hat{\mathbf{K}}_{c,d}(n) &= \frac{1}{N}\sum_m \mathbf{K}_{c,d}(m) e^{i2\pi\frac{nm}{N}}\\ &= \frac{1}{N} \sum_m \sum_{\alpha,\beta,\alpha - \beta= m}\mathbf{P}_{(c,\alpha), (d, \beta)} e^{i2\pi\frac{nm}{N}}\\ &= \frac{1}{N} \sum_{\alpha,\beta}\mathbf{P}_{(c,\alpha), (d, \beta)} e^{i2\pi\frac{n(\alpha-\beta)}{N}}\\ \end{split} \end{equation}

where NN is the number of spatial locations. Here we eliminate mm by re-grouping elements according to the α\alpha and β\beta. Recall that P=(V∥V∥H)∗\mathbf{P} =\left(\mathbf{V}_{\parallel}\mathbf{V}_{\parallel}^H\right)^*:

P(c,α),(d,β)=∑kvk∗(c,α)vk(d,β)\begin{equation} \begin{split} \mathbf{P}_{(c,\alpha), (d, \beta)} &= \sum_k \mathbf{v}_k^*(c,\alpha)\mathbf{v}_k(d,\beta) \end{split} \end{equation}

where vk(c,α)\mathbf{v}_k(c,\alpha) represents a scalar value of the coil cc and location α\alpha of the kk-th component of V∥\mathbf{V}_{\parallel}. Then we have:

K^c,d(n)=1N∑α,βP(c,α),(d,β)ei2πn(α−β)N=N∑k(1N∑αvk∗(c,α)ei2πnαN)(1N∑βvk(d,β)e−i2πnβN)=N∑kv^k(c,n)v^k∗(d,n)\begin{equation} \begin{split} \hat{\mathbf{K}}_{c,d}(n) &= \frac{1}{N} \sum_{\alpha,\beta}\mathbf{P}_{(c,\alpha), (d, \beta)} e^{i2\pi\frac{n(\alpha-\beta)}{N}}\\ &= N \sum_k \left(\frac{1}{N} \sum_{\alpha} \mathbf{v}_k^*(c, \alpha)e^{i2\pi\frac{n\alpha}{N}}\right)\left(\frac{1}{N} \sum_{\beta} \mathbf{v}_k(d, \beta)e^{-i2\pi\frac{n\beta}{N}}\right)\\ &= N \sum_k \hat{\mathbf{v}}_k(c, n)\hat{\mathbf{v}}_k^*(d, n) \end{split} \end{equation}

where v^k(c,n)\hat{\mathbf{v}}_k(c, n) is the inverse Fourier transform of the conjugated vk(c,m)\mathbf{v}_k(c, m) at the location nn.

Substituting equation (24) into equation (21):

M−1NGnGnH[s1(n)⋮sNc(n)]=[s1(n)⋮sNc(n)]\begin{equation} \begin{split} M^{-1}N \mathbf{G}_n \mathbf{G}_n^H \begin{bmatrix} \mathbf{s}_1(n)\\ \vdots\\ \mathbf{s}_{N_c}(n)\\ \end{bmatrix} &= \begin{bmatrix} \mathbf{s}_1(n)\\ \vdots\\ \mathbf{s}_{N_c}(n)\\ \end{bmatrix} \end{split} \end{equation}

where Gn=M−1/2N1/2[v^1(1,n)⋯v^Nk(1,n)⋮⋱⋮v^1(Nc,n)⋯v^Nk(Nc,n)]\mathbf{G}_n = M^{-1/2}N^{1/2}\begin{bmatrix} \hat{\mathbf{v}}_1(1, n) & \cdots & \hat{\mathbf{v}}_{N_k}(1, n)\\ \vdots & \ddots & \vdots\\ \hat{\mathbf{v}}_1(N_c, n) & \cdots & \hat{\mathbf{v}}_{N_k}(N_c, n)\\ \end{bmatrix}.

Let’s summarize the steps to compute coil sensitivities:

  1. Reshape V∥\mathbf{V}_{\parallel} to the shape P×Nc×NkP \times N_c \times N_k
  2. Center it and pad it to the full-grid size N×Nc×NkN \times N_c \times N_k
  3. Apply the inverse Fourier transform on the conjugated k-space kernels
  4. Extract Gn\mathbf{G}_n of shape Nc×NkN_c \times N_k for each pixel nn
  5. Compute eigenvectors of M−1NGnGnHM^{-1}N\mathbf{G}_n\mathbf{G}_n^H
  6. Select the eigenvectors corresponding to the eigenvalues of 1, which represent the coil sensitivities at pixel nn
  7. Repeat 4 to 6 until all pixels have been processed

Connections to the “kernel flippling” operation

Most implementations would do the following kernel flipping operation before applying the Fourier transform:

KERNEL = zeros(imSize(1), imSize(2), size(kernel,3), size(kernel,4));
for n=1:size(kernel,4)
    KERNEL(:,:,:,n) = (fft2c(zpad(conj(kernel(end:-1:1,end:-1:1,:,n))*sqrt(imSize(1)*imSize(2)), ...
        [imSize(1), imSize(2), size(kernel,3)])));
end

Instead, our algorithm suggests that:

KERNEL = zeros(imSize(1), imSize(2), size(kernel,3), size(kernel,4));
for n=1:size(kernel,4)
    KERNEL(:,:,:,n) = (ifft2c(zpad(conj(kernel)*sqrt(imSize(1)*imSize(2)), ...
        [imSize(1), imSize(2), size(kernel,3)])));
end

By using the shift properties of the Fourier transform, We can show that:

ifft(ifftshift(x))[m]=ei2πmN(2⌈N/2⌉−1)fft(ifftshift(xrev∗))\begin{equation} \begin{split} ifft(ifftshift(x))[m] = e^{i2\pi \frac{m}{N} (2\lceil N/2\rceil -1)} fft(ifftshift(x^*_{rev})) \end{split} \end{equation}

where xrev∗x^*_{rev} is the conjugate of the reversed signal xx. If NN is odd, our implementation is equivalent to the kernel flipping operation. However, if NN is even, there exists a linear phase term e−i2πmNe^{-i2\pi \frac{m}{N}} between the two methods.

I am still investigating the differences between the two methods. However, based on the assumptions in the original paper, I ended up with algorithmic steps that, for unknown reasons, do not match those in other offical implementaions such as bart.

I believe Professor Haldar’s linear-predictability framework may help explain the discrepancy here. In that work, the authors present a connection between ESPIRiT and the nullspace algorithm direclty, but without providing a proof. Surprisingly, one of their acceleration techniques(Section IV, Part C) is quite similar to my relative shift trick in equation (18). I plan to explore the underlying mathematical relationships in my next blog post.